En multitud de situaciones y sucesos de muy diversas características el hombre ha podido percatarse que los valores de una cierta cantidad 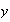depende de los de otra cantidad 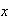del modo anteriormente descrito, es decir: a cada valor de le corresponde un único valor de .

• El área de un cuadrado depende de la longitud de su lado:
  

  

• La rapidez con que un cuerpo recorre una distancia de kilómetros depende del tiempo que emplea para hacerlo:
  

  

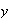En todos estos casos decimos que 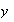varía con 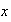y de manera más precisa que 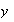es función de 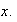Además, 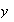es entonces llamada la variable dependiente y 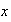la variable independiente.

Una de nuestras herramientas más poderosas para entender nuestro entorno es la colección de fórmulas que hemos podido establecer para relacionar diversas cantidades que nos interesan en momentos o situaciones particulares.

Lo anterior llevó a introducir la noción matemática de función. De una manera un tanto informal decimos:

Definición

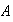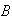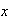Se establece una función de un conjunto en un conjunto , cuando se da una regla (criterio o ley) a través de la cual asociamos a cada elemento de 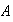un único elemento 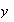de 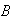; a dicha regla se le denomina la regla de correspondencia o de asociación de la función y se le denota por una letra, digamos 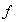. Todo esto se resume con la siguiente notación: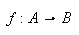

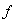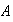Observamos que para tener una función, debemos tener 2 conjuntos, que pueden ser iguales entre sí, y una regla de correspondencia con las características antes descritas. Cuando no hay lugar a confusión, nos referimos a una función mediante la letra que usamos para su regla de correspondencia; por ejemplo, en el caso que nos ocupa podemos hablar simplemente de la función . El conjunto es llamado el dominio de la función y para señalarlo escribimos 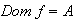. 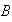El conjunto es llamado el codominio o contradominio de la función

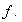
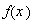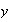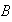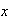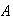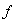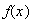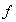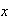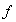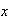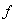Se acostumbra denotar por al elemento de que está asociado al elemento de a través de . Usamos las siguientes expresiones para referirnos a : de , en , el valor que toma en 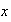y la imagen de 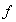en

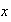
En la siguiente escena, introduce una expresión algebraica en el campo que está abajo a la derecha. Utiliza * para indicar multiplicación, / para división y 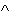para exponenciación.

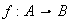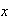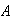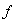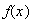Cuando se tiene una función y en , también se acostumbra decir que envía a en o 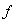transforma a 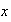en 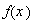y escribir .

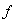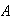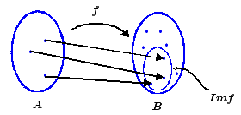
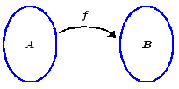
La primera de estas dos últimas expresiones nos sugiere usar la siguiente: envía a los elementos de en 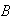y nos lleva a considerar que la función es un utensilio que envía, "dispara" o "proyecta" objetos de un conjunto sobre objetos de otro conjunto; esto queda reflejado mediante el siguiente diagrama, mismo que con frecuencia se usa para indicar que hay una función .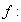

La segunda expresión da la idea de que una función actúa a manera de un artefacto que al introducirle un elemento de un conjunto produce un elemento de un conjunto , de la misma manera que una máquina transforma los insumos en un producto final. Todas estas imágenes son aceptables si nos ayudan a manejar el concepto de función.

Ejemplos

1. Determinar si el siguiente diagrama corresponde a una función del conjunto , que tiene tres puntos, en el conjunto de , que consta de cuatro.

   Solución
   

   
   

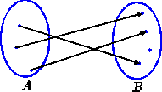
   Como a cada elemento de se le asocia un único elemento de , entonces el diagrama sí corresponde a una función. El hecho de que hay un elemento en 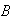que no es el asociado de un punto de 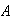no contradice la definición, pues en ésta no se exige que cada elemento de 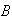sea el asociado de un elemento de .

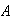2. Determinar si el siguiente diagrama corresponde a una función.
   

   
   

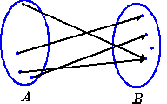
   Solución

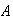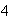   Como cada elemento del conjunto , compuesto por puntos, tiene asociado un único elemento de 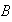, entonces el diagrama sí corresponde a una función.

   En este ejemplo sucede que dos elementos de tienen asociado el mismo elemento de

3. Determinar si el siguiente diagrama corresponde a una función.
   

   
   

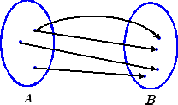
   Solución

   Puesto que hay un elemento del dominio que tiene asociado a dos elementos del contradominio, distintos entre sí, el diagrama no corresponde a una función.

Definición

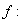
Para cualquier función 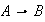, definimos la imagen o rango de la función 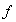como la colección de todos los elementos 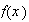, con 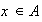, es decir, todos aquellos elementos de 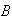que fueron los asociados a los elementos de 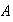. Este conjunto se denota por 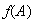o bien .

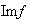Es claro que

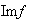
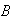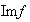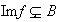es un subconjunto del codominio y puede suceder que sea un subconjunto propio del codominio, es decir, que sea un subconjunto del codominio que no coincida con él, lo cual se denota por ; tal es el caso para la función representada en la siguiente figura: