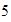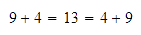Las dos operaciones principales de los números enteros son la suma y el
producto. El producto también se conoce como multiplicación. Veamos
primero una interpretación geométrica de la suma.
Para hallar la suma de
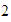 y
y
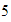 ,
dibujamos una recta numérica. Colocamos el lápiz en el
,
dibujamos una recta numérica. Colocamos el lápiz en el
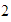 y nos movemos
y nos movemos
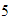 unidades hacia la derecha, con lo que llegamos al
unidades hacia la derecha, con lo que llegamos al
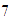 .
.
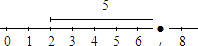
Suma de
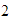 y
y
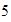
Cuando a un número le sumamos un número positivo,
entonces nos movemos hacia la derecha y cuando le sumamos un
número negativo, entonces nos movemos hacia la
izquierda.
Ejemplos
-
Sumar
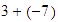 .
.
Solución:
Localizamos el
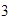 y desde ahí nos movemos
y desde ahí nos movemos
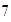 unidades hacia la izquierda, con lo que llegamos a
unidades hacia la izquierda, con lo que llegamos a
 Así que
Así que
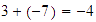 .
.
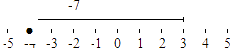
Suma de
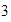 y
y
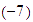
-
Sumar
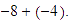
Solución:
Localizamos a
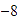 y desde ahí nos movemos
y desde ahí nos movemos
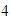 unidades hacia la izquierda, con lo que llegamos a
unidades hacia la izquierda, con lo que llegamos a
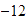 .
Así que
.
Así que
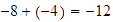 .
.
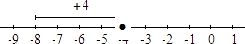
Suma de
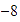 y
y
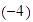
Sería poco práctico tener que utilizar la recta numérica para
poder sumar enteros positivos y negativos; las siguientes reglas nos permiten
hacerlo de manera sencilla, usando lo aprendido en la escuela primaria.
Reglas para sumar números enteros
-
Se suman los valores absolutos de los números, es decir, como si fueran
positivos
-
Se determina el signo de la suma:
- a.
-
Si ambos son positivos, la suma es positiva.
- b.
-
Si ambos son negativos, la suma es negativa.
Ejemplo
-
Sumar
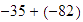 .
.
Solución:
Sumamos valores absolutos de los números:
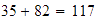 .
.
La suma es negativa ya que ambos son negativos:
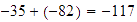 .
.
-
Para sumar dos números enteros de signo contrario:
-
Se restan los valores absolutos de los números: el menor del mayor.
-
El signo de la suma es el signo del sumando que tenga el mayor valor absoluto
.
Ejemplos
-
Sumar
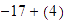 .
.
Solución:
El valor absoluto de
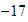 es
es
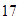 ,
que es mayor que el de
,
que es mayor que el de
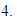
Restamos los valores absolutos:
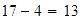 .
.
La suma es negativa porque
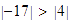 ;
así,
;
así,
 .
.
-
Sumar
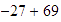 .
.
Solución:
El valor absoluto de
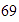 es mayor que el de
es mayor que el de
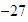 .
.
Restamos los valores absolutos:
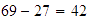 .
.
La suma es positiva porque
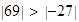 ;
así,
;
así,
 .
.
Desde que aprendimos a sumar en la primaria, nos enseñaron que al sumar
dos números, no importa el orden en el que los sumemos; así:
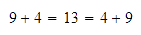
y al sumar más de dos números, lo que debemos hacer es agrupar dos
de ellos, sumarlos y el resultado sumarlo al resto, por ejemplo: la suma
 la podemos realizar de las siguientes dos
maneras:
la podemos realizar de las siguientes dos
maneras:
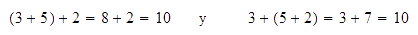
y
simplemente
escribimos
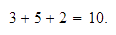
También sabemos que sumar
 ''no hace nada'':
''no hace nada'':

Propiedades de la suma de números enteros
A continuación se enlistan las propiedades de suma de los números
enteros que acabamos de ejemplificar.
La suma de números enteros satisface las siguientes propiedades:
Observaciones
-
Los números naturales
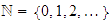 satisfacen todas las propiedades anteriores con excepción de la
existencia del inverso aditivo, ya que, por ejemplo, el inverso aditivo
de
satisfacen todas las propiedades anteriores con excepción de la
existencia del inverso aditivo, ya que, por ejemplo, el inverso aditivo
de
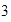 es
es
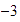 ,
que no es un número natural.
,
que no es un número natural.
-
El símbolo
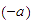 significa el inverso aditivo de
significa el inverso aditivo de
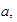 independientemente de que
independientemente de que
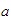 sea positivo o negativo. Así por ejemplo, como
sea positivo o negativo. Así por ejemplo, como
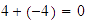 ,
entonces el inverso aditivo de
,
entonces el inverso aditivo de
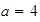 es
es
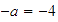 ,
pero también, el inverso aditivo de
,
pero también, el inverso aditivo de
 es
es
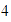 ,
es decir,
,
es decir,
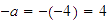 .
.
En general, si
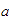 es un número entero, entonces
es un número entero, entonces
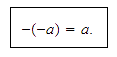
Ejemplos
-
El opuesto de
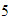 es
es
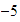 .
.
-
El opuesto de
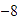 es
es
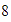 .
.
-
El opuesto de
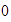 es
es
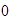 .
.
-
Verificar geométricamente la propiedad conmutativa con
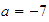

Solución:
Localizamos
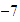 y desde ahí nos movemos
y desde ahí nos movemos
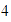 unidades a la derecha y llegamos a
unidades a la derecha y llegamos a
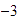 .
.
Localizamos a
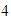 y desde ahí nos movemos
y desde ahí nos movemos
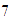 unidades a la izquierda y llegamos también a
unidades a la izquierda y llegamos también a
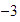 .
Así
.
Así 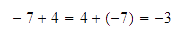
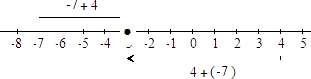
-
Verificar geométricamente la propiedad asociativa con
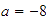 ,
,
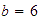 y
y
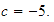
Solución:
Para sumar
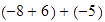 ,
a partir de
,
a partir de
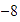 nos movemos
nos movemos
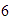 unidades a la derecha, llegamos a
unidades a la derecha, llegamos a
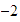 ,
y si desde ahí nos movemos
,
y si desde ahí nos movemos
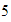 unidades a la izquierda, llegamos a
unidades a la izquierda, llegamos a
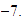
Para sumar
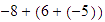 ,
efectuamos primero
,
efectuamos primero
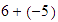 ,
con lo que nos colocamos en
,
con lo que nos colocamos en
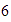 y de ahí nos movemos
y de ahí nos movemos
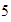 unidades a la izquierda, con lo cual llegamos a
unidades a la izquierda, con lo cual llegamos a
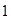 .
Ahora, si a partir de
.
Ahora, si a partir de
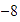 nos movemos
nos movemos
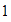 unidad a la derecha, llegamos a
unidad a la derecha, llegamos a
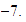 Así que
tenemos:
Así que
tenemos:
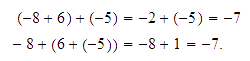
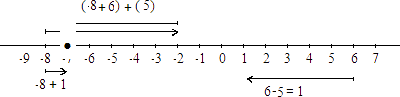
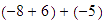
- Verificar geométricamente las propiedades del neutro y del inverso
aditivo con el número
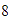 .
.
Solución:
Localizamos el
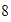 y no nos movemos, entonces seguimos en el
y no nos movemos, entonces seguimos en el
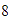 ,
así que
,
así que
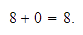
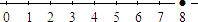
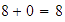
Para ver la propiedad del opuesto, localizamos el
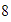 y nos movemos
y nos movemos
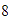 unidades hacia la izquierda con lo que llegamos a
unidades hacia la izquierda con lo que llegamos a
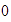 ,
así:
,
así:
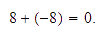
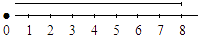
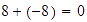 .
.
Las propiedades conmutativa y asociativa, así como las reglas anteriores
nos permiten sumar más de dos números enteros.
Ejemplo
-
Sumar
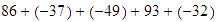 .
.
Solución:
Aplicamos la propiedad conmutativa para poner todos los números positivos
juntos y todos los números negativos juntos.
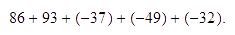
Sumamos
por separado los números positivos y los números negativos siguiendo
las reglas para sumar números del mismo signo:
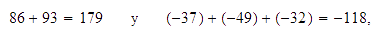
sumamos
estos resultados parciales
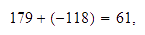
así,
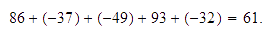





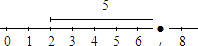
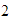 y
y