• Cuando discutimos sobre la belleza de dos artistas de cine, no siempre llegamos a un acuerdo, ``en gustos se rompen géneros''; en cambio, dados dos números naturales, siempre podemos decidir cuál de ellos es mayor, por ejemplo, 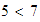. Esto ejemplifica la propiedad conocida como tricotomía.

• Cuando comparamos a tres equipos de fútbol, tampoco podemos decir siempre cuál es el mejor. Por ejemplo, en un torneo de todos contra todos, los Pumas le ganaron a las Aguilas, las Aguilas le ganaron a las Chivas y las Chivas le ganaron a los Pumas, así que no podemos decidir cuál es mejor. En cambio, con los números no hay tal ambigüedad, por ejemplo, si sabemos que 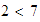y 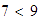, sin pensarlo más sabemos que . Es decir, el orden en los números naturales es transitivo.

• Si Cristina es mayor que su hermano Juan, entonces dentro de cinco años, Cristina seguirá siendo mayor que Juan, es decir, si a la edad de ambos le sumamos 5, el orden no se altera.

• Si un refresco es más barato que una bolsa de papas y, debido a la inflación, el año próximo el precio de ambos se multiplica por 2, entonces el refresco seguirá siendo más barato que la bolsa de papas.

Para poder comparar los números, debemos establecer sin ambigüedad un orden entre ellos. Para ello, hacemos lo siguiente:

Definición

Dados dos números enteros y 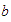, decimos que 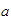es menor que 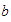si al colocarlos en la recta, 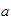queda a la izquierda de 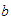, y escribimos 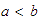, que se lee '' 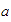es menor que 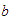'' o '' 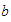es mayor que ''

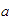Otra manera de escribir 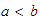es 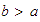, en cuyo caso leemos " 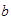es mayor que ".

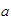Escribimos 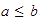para indicar que 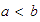, o bien 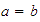, y leemos " es menor o igual que ".

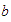Ejemplos

• canicas son más que canicas.

• $ es menor que $ , (se tiene menos dinero cuando se debe que cuando se debe ).

• C es menor que C, ya que es más alta la temperatura a C que a C.

Podemos escribir las desigualdades anteriores así

:

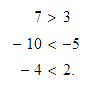
Propiedades de orden de los enteros

El orden en los enteros satisface las siguientes propiedades:

• Tricotomía

  Dados y números enteros, se cumple exactamente una de las siguientes afirmaciones



Decir que es positivo equivale a decir que ; y que es negativo equivale a decir que .

• Transitividad

  Si y , entonces .

  Es decir, si está a la izquierda de y está a la izquierda de , entonces está a la izquierda de .

• Relación con la suma

  Si y es cualquier entero, entonces .

• Multiplicación por un número positivo

  Si y es cualquier entero positivo, entonces . (No se altera el sentido de la desigualdad).

• Multiplicación por un número negativo. Si y entonces . (Se invierte el sentido de la desigualdad).

Ejemplos

1. Verificar la transitividad cuando 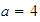, 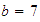y .

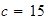   Solución:

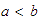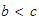   Debemos verificar que: si y , entonces 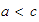. En efecto



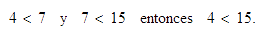
2. Multiplica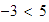r por .

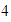   Solución:

   Al multiplicar una desigualdad por un número positivo, el sentido de la desigualdad no se altera, así que



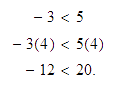
3. Multiplica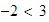r por .

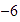   Solución:

   Puesto que vamos a multiplicar por un número negativo, debemos recordar que al hacerlo se debe intercambiar el signo por . Entonces



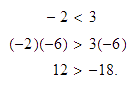
4. Mostrar que la desigualdad 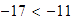se puede obtener a partir de la desigualdad .

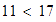   Solución:

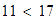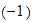   Puesto que , multiplicando por a ambos lados de la desigualdad tenemos:



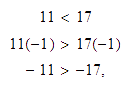
o lo que es lo mismo, 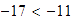.