Si tenemos
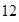 mosaicos cuadrados y deseamos formar un rectángulo con ellos, entonces
podemos hacerlo de diversas
maneras:
mosaicos cuadrados y deseamos formar un rectángulo con ellos, entonces
podemos hacerlo de diversas
maneras:
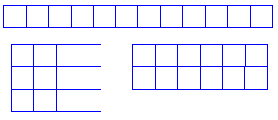
En cambio, si tenemos
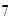 mosaicos cuadrados, sólo podemos acomodarlos de una manera para obtener
un rectángulo
mosaicos cuadrados, sólo podemos acomodarlos de una manera para obtener
un rectángulo

La diferencia entre
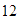 y
y
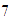 es que podemos factorizar el
es que podemos factorizar el
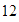 de varias maneras:
de varias maneras:
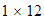 ,
,
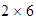 ,
,
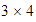 ;
en cambio, el
;
en cambio, el
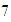 únicamente podemos factorizarlo como
únicamente podemos factorizarlo como
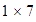 .
.
Factorizar un número natural significa expresarlo como producto de otros
números naturales.
Un número primo es un número natural mayor que 1
cuyos únicos factores son 1 y él mismo. También podemos decir
que un número es primo si es mayor que 1 y tiene exactamente
dos factores distintos: el
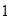 y él mismo.
y él mismo.
Los primeros números primos son:
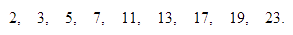
Un número mayor que uno, que no es un número primo, se llama
número compuesto.
Un número que es factor de dos o más números se llama
factor común de ellos.
Ejemplos
-
Encontrar los factores primos de
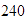 ,
todos sus factores y escribirlo como producto de potencias de primos.
,
todos sus factores y escribirlo como producto de potencias de primos.
Solución:
-
Factorizamos:
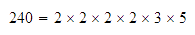
entonces
sus factores primos son 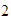 ,
, 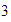 y
y 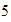 .
.
-
Todos sus factores
son:
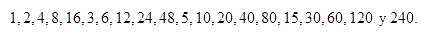
-
Su factorización en producto de potencias de primos es:
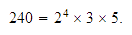
-
Encontrar los factores primos de
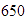 ,
todos sus factores y escribirlo como producto de potencias de primos.
,
todos sus factores y escribirlo como producto de potencias de primos.
Solución:
-
Encontrar los factores comunes de
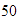 y
y
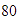 .
.
Solución:
Los factores de
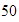 son:
son: 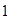 ,
, 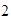 ,
, 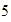 ,
, 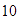 ,
, 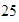 y
y 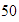 .
.
Los factores de
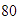 son:
son: 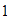 ,
, 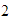 ,
, 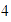 ,
, 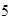 ,
, 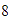 ,
, 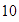 ,
, 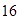 ,
, 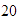 ,
, 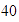 y
y 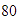 .
.
Los números que aparecen en ambas listas, es decir, los factores comunes
son: 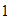 ,
, 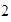 ,
, 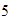 y
y 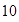 .
.
-
Encontrar los factores comunes de
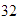 y
y
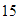 .
.
Solución:
Los factores de
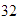 son:
son:
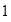 ,
,
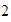 ,
,
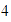 ,
,
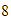 ,
,
 y
y
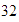 .
.
Los factores de
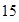 son:
son:
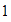 ,
,
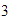 ,
,
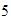 y
y
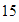 .
.
El único número factor común es
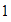 .
.
Cuando el único factor común que tienen dos números es el
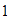 ,
decimos que los números son primos entre sí o primos
relativos.
,
decimos que los números son primos entre sí o primos
relativos.
El Máximo Factor Común (MFC) o Máximo Común
Divisor (MCD) de dos o más números es el máximo de sus
factores comunes.
Para encontrar el máximo común divisor de dos números, podemos
utilizar cualquiera de los siguientes métodos.
-
Encontrar las lista de todos los factores de cada número, fijarse en los
comunes a ambas listas y elegir el mayor de ellos. Este número es el MCD
de los números dados. Si el único número que está en ambas
listas es el 1, entonces el MCD de ellos es 1, es decir, los números son
primos entre sí.
-
Encontrar las descomposiciones en potencias de primos de ambos números.
Considerar aquellos primos que son factores de ambos números. Para cada
uno de éstos, comparar sus exponentes y elegir el menor de ellos. El
producto de dichos primos elevados a los menores exponentes es el MCD de los
números dados.
-
Algoritmo de Euclides. Se divide el número mayor entre
el menor. Si el residuo no es cero, se divide el divisor anterior entre el
residuo obtenido y se continúa de esta manera hasta que el residuo es
cero. El último residuo distinto de cero es el MCD de los números
dados.
Ejemplo
El
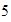 es último residuo distinto de cero, así que el MCD de
es último residuo distinto de cero, así que el MCD de 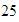 y
y
 es
es
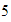 .
.




